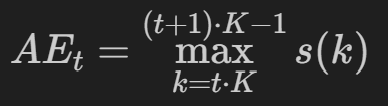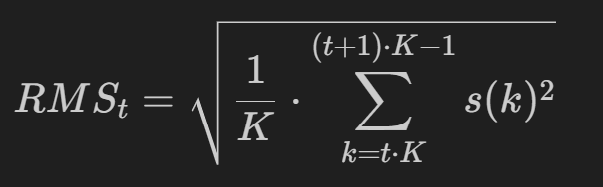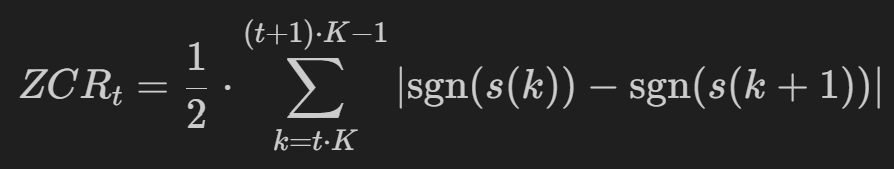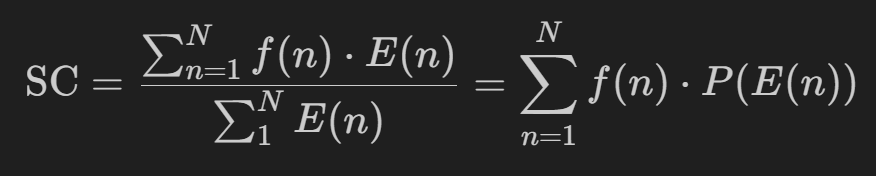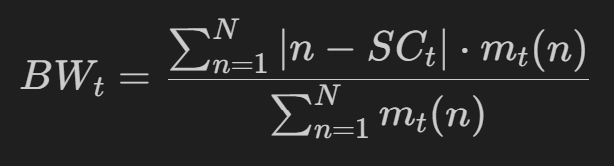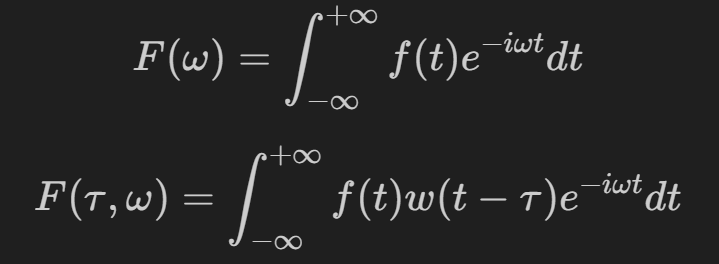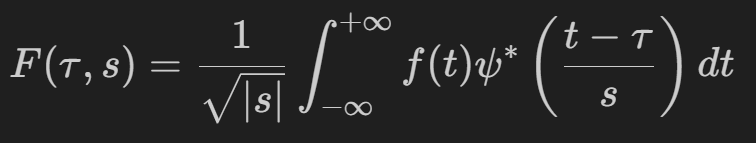音频信号处理及深度学习教程（已完结）

音频信号处理及深度学习教程

Posted Apr 22, 2025 Updated May 5, 2025

By Zhai Wangyuxuan

33 min read

音频信号处理及深度学习教程（已完结）

课程链接

课程内容

音频信号处理
Pytorch环境介绍
机器学习与深度学习原理
Torchaudio应用
基于音频的深度学习应用

PART 1 - 信号分析

第一章信号分析简介

信号分析是什么

信号分析：将一个复杂信号分解成若干简单信号分量之和，或者用有限的一组参量去表示一个复杂波形的信号，从这些简单的分量组成情况去考察复杂信号的特性；
特征提取的过程：从一段复杂的波形中提取出我们需要的信息。

为什么要分析信号

获取信号特征信息得到复杂信号的基本特征；
获取信号源特征信息；
深度学习的第一步都是要收集数据集的特征(feature)。

信号分析方式

信号平稳：可以在时域和频域直接分析；
信号不平稳：将信号拆解分析，可分为时域、频域与时频域。

多个信号的叠加

参考三角变换公式；
低频信号：决定信号的包络形状；
高频信号：决定信号的精细结构；
ASP 中，通常用包络形状来区分不同音频信号，因此更关注低频信号。

第二章信号的时域分析幅值包络

信号的时域分析

幅值包络

操作：依次寻找每一帧中的幅值最大值，将每一帧中幅值最大值连起来就是幅值包络。

对于每一帧，找到该帧中信号幅值的最大值。将每一帧的最大值作为该帧的幅值包络值。

分帧概念

分帧：若不考虑分帧重叠，帧的个数 frame_num = 总采样点数 ÷ 帧长；
分帧重叠：若采用重叠分帧，设重叠长度 hop_size 为 128 个采样点。下一帧会包含上一帧的 128 个采样点，能让信号处理更平滑；
分帧补零：帧个数 frame_num = 总采样数 ÷ 重叠长度。可能无法整除，故向上取整。通过补零可让这些零散采样点也能参与后续处理。

代码演示

  
# 0. 预设环境
import librosa
import librosa.display
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns

# 1. 加载信号
wave_path = "D:/02-programme_BJTU_New/DeepLearning/ASP_DL/test_audio.mp3"
wave_path_relative = "DeepLearning/ASP_DL/test_audio.mp3"
waveform, sample_rate = librosa.load(wave_path, sr = None)

# 2. 定义一个 AE 的函数，功能为提取信号中每一帧中最值，结合成为包络
def Calc_Amplitude_Envelope(waveform, frame_length, hop_length):
    
    if len(waveform) % hop_length != 0:
        frame_num = int((len(waveform) - frame_length) / hop_length) + 1
        pad_num = frame_num + hop_length + frame_length - len(waveform)
        waveform = np.pad(waveform, (0, pad_num), mode = "wrap")
    
    frame_num = int((len(waveform) - frame_length) / hop_length) + 1
    waveform_ae = []

    for t in range(frame_num):
        # current_frame = waveform[t * (frame_length - hop_length) : t * (frame_length - hop_length) + frame_length]
        current_frame = waveform[t * hop_length: t * hop_length + frame_length]
        current_ae = max(current_frame)
        waveform_ae.append(current_ae)

    return np.array(waveform_ae)

# 3. 设置参数，每一帧长 1024，以 50% 的重叠率分帧，调用该函数
frame_size = 1024
hop_size = int(frame_size * 0.5)
waveform_AE = Calc_Amplitude_Envelope(waveform = waveform, frame_length = frame_size, hop_length = hop_size)

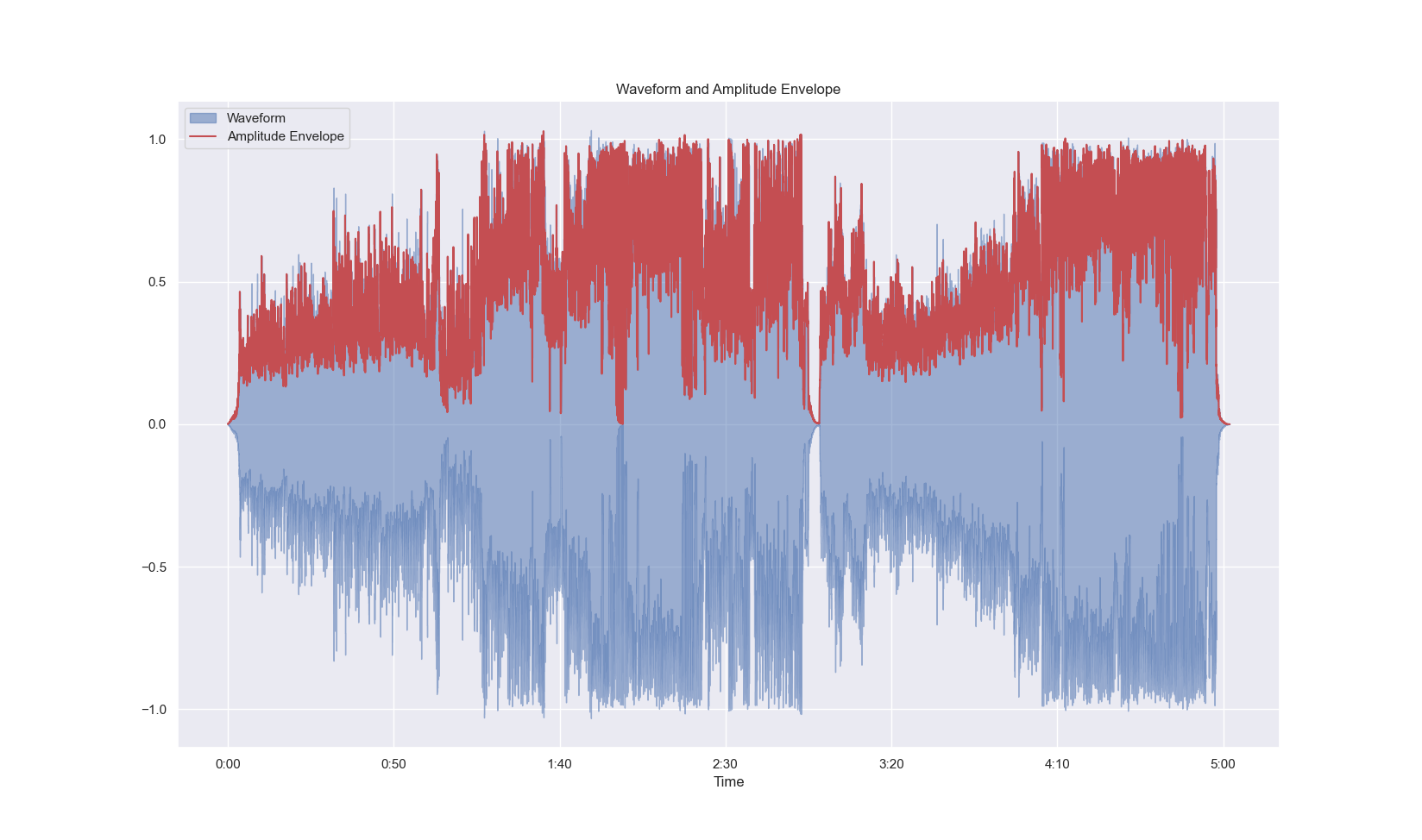
# 4. 绘制信号和幅值包络信息在同一张图中
frame_scale = np.arange(0, len(waveform_AE))
time_scale = librosa.frames_to_time(frame_scale, sr=sample_rate, hop_length=hop_size)

sns.set_theme()
plt.figure(figsize=(20, 10))
librosa.display.waveshow(waveform, sr=sample_rate, alpha=0.5, label="Waveform")
plt.plot(time_scale, waveform_AE, color="r", label="Amplitude Envelope")
plt.title("Waveform and Amplitude Envelope")
plt.legend()
plt.show()

第三章信号分析简介

均方根能量 Root mean square energy

考察每一帧的包络变化，适用于不平稳的信号，尤其是对于突变信号；RMSE 得到的值较为平稳，因为它利用了每一帧的所有点幅值的平均值，而非 AE 中利用每一帧的最大幅值；
应用：RMSE 与响度有关，用于音频分段、分类

代码演示

  
'''
# 0.预设环境
# 1.加载信号
# 2.定义函数 RMS, 功能:计算每一帧的均方根能量, 公式 = 该帧信号的平方和, 取帧长的平均值后, 开根号后
# 3.设置参数:每一帧长 1024, 以 50% 的重叠半分帧, 调用该函数
# 4.绘制图像
# 5.利用 librosa.feature.rms 绘制信号的RMS
# 6.比较两者差异
'''

# 0.预设环境
import librosa
import numpy as np
from matplotlib import pyplot as plt
import librosa.display
import seaborn as sns

sns.set()

# 1.加载信号
wave_path = "D:\\02-programme_BJTU_New\\DeepLearning\\ASP_DL\\test_audio.mp3"
waveform, sample_rate = librosa.load(wave_path, sr=None)

# 2.定义函数 RMS，功能，计算每一帧的均方根能量
def Calc_RMS(waveform, frame_length, hop_length):

    if len(waveform) % hop_length != 0:
        frame_num = int((len(waveform) - frame_length) / hop_length) + 1
        pad_num = frame_num * hop_length + frame_length - len(waveform)
        waveform = np.pad(waveform, pad_width=(0, pad_num), mode="wrap")

    frame_num = int((len(waveform) - frame_length) / hop_length) + 1
    waveform_rms = []

    for t in range(frame_num):
        current_frame = waveform[t * (frame_length - hop_length): t * (frame_length - hop_length) + frame_length]
        current_rms = np.sqrt(np.sum(current_frame**2) / frame_length)
        waveform_rms.append(current_rms)

    return np.array(waveform_rms)

# 3.设置参数:每一帧长 1024, 以 50% 的重叠半分帧, 调用该函数
frame_size = 1024
hop_size = int(frame_size * 0.5)
waveform_RMS = Calc_RMS(waveform, frame_size, hop_size)

# 4.绘制图像
# 计算手动计算的 RMS 的时间刻度
frame_scale = np.arange(0, len(waveform_RMS), step=1)
time_scale = librosa.frames_to_time(frame_scale, sr=sample_rate, hop_length=hop_size)

plt.figure(figsize=(20, 10))
librosa.display.waveshow(waveform, sr=sample_rate)
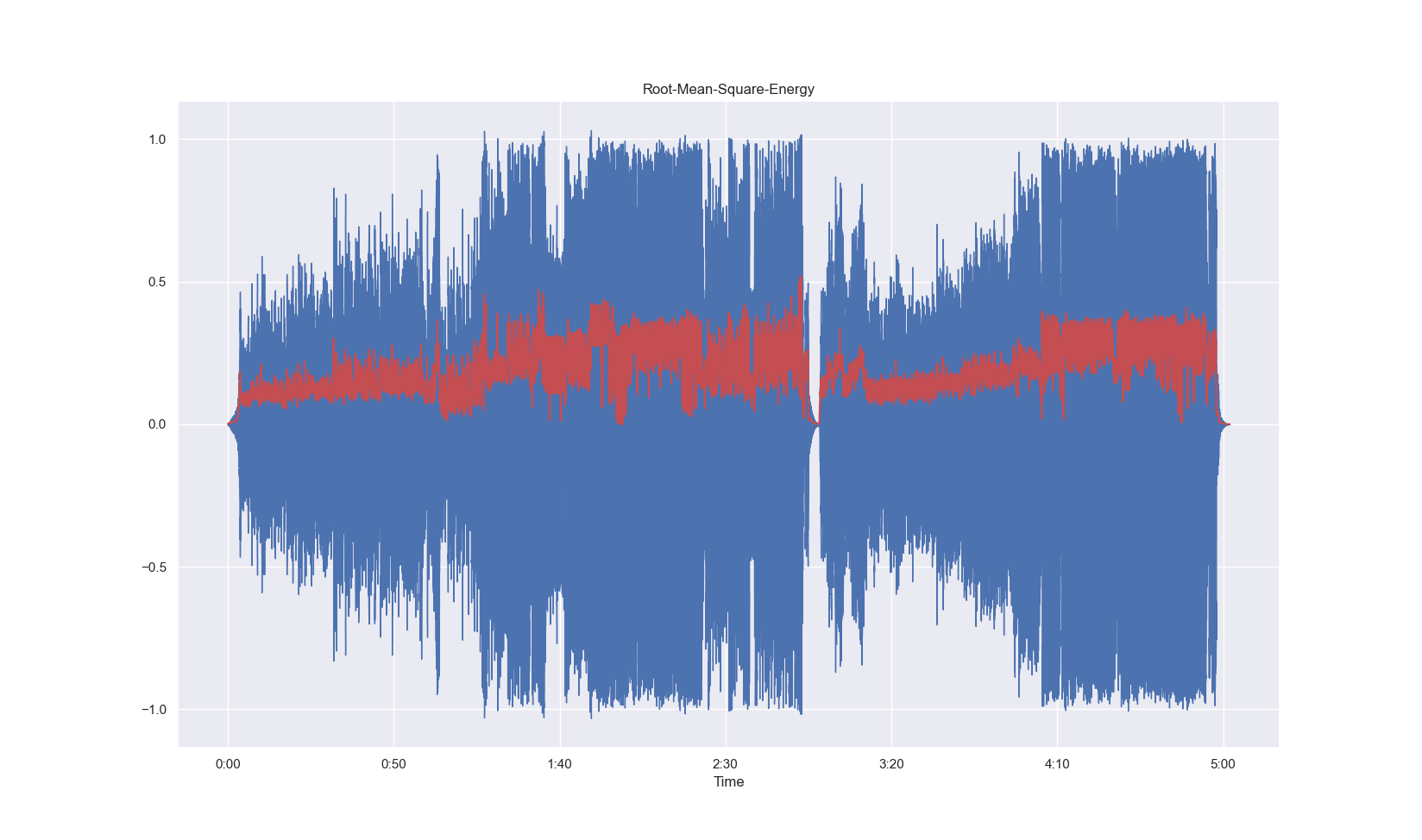
plt.plot(time_scale, waveform_RMS, color="r")
plt.title("Root-Mean-Square-Energy")
plt.show()

# 5.利用 librosa.feature.rms 绘制信号的RMS
waveform_RMS_librosa = librosa.feature.rms(y=waveform, hop_length=hop_size, frame_length=frame_size).T[1:, 0]

# 确保 librosa 计算的 RMS 的时间刻度长度与波形长度一致
librosa_frame_scale = np.arange(0, len(waveform_RMS_librosa), step=1)
librosa_time_scale = librosa.frames_to_time(librosa_frame_scale, sr=sample_rate, hop_length=hop_size)

plt.figure(figsize=(20, 10))
librosa.display.waveshow(waveform, sr=sample_rate)
plt.plot(librosa_time_scale, waveform_RMS_librosa, color="r")
plt.title("Root-Mean-Square-Energy_librosa")
plt.show()

# 确保比较的数组长度一致
min_length = min(len(waveform_RMS), len(waveform_RMS_librosa))
bias = waveform_RMS_librosa[:min_length] - waveform_RMS[:min_length]
print(f"the bias is {bias}\n Congratulation!")

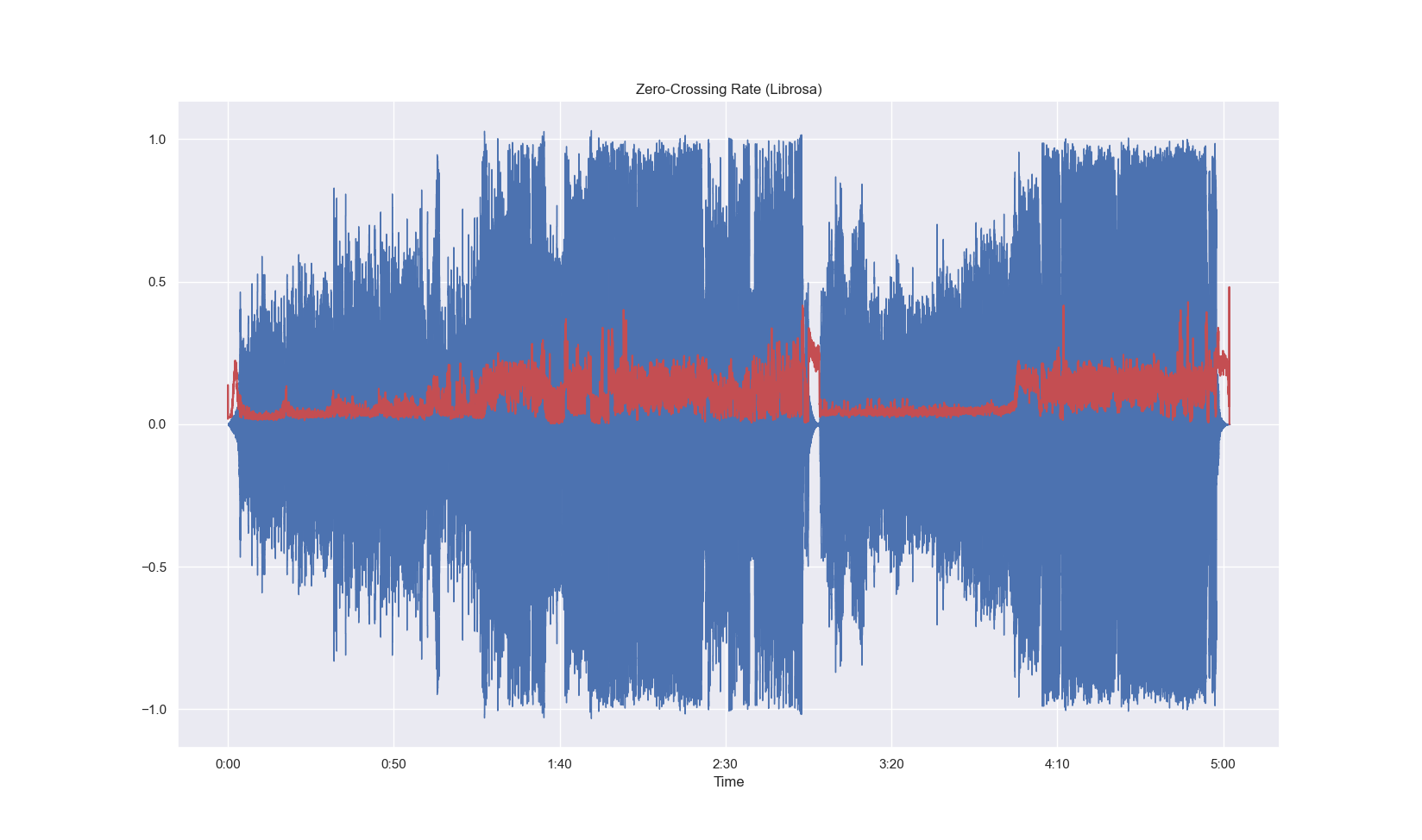
第四章信号的时域分析过零率

每帧中语音信号从正变为负或从负变为正的次数

代码演示

  
'''
信号的过零率ZCR
0.预设环境
1.加载信号
2.定义函数, 功能: 计算每一帧的过零率
np.sum(np.abs(np.sign(a)-np.sign(b))))/2/frame_leength
3.设置参数:每一帧长1024,以50%的重叠率分帧,调用该函数
4.绘制图像
5.利用自带函数
6.比较差异
'''

# 0.预设环境
import librosa
import numpy as np
from matplotlib import pyplot as plt
import librosa.display
import seaborn as sns

sns.set()

# 1.加载信号
wave_path = "D:\\02-programme_BJTU_New\\DeepLearning\\ASP_DL\\test_audio.mp3"
waveform, sample_rate = librosa.load(wave_path, sr = None) # 获得波形与采样率

# 2.定义函数, 功能: 计算每一帧的过零率
def Calc_ZCR(waveform, frame_length, hop_length):

    if len(waveform) % hop_length != 0:
        frame_num = int((len(waveform) - frame_length) / hop_length) + 1
        pad_num = frame_num * hop_length + frame_length - len(waveform)
        waveform = np.pad(waveform, pad_width = (0, pad_num), mode = "wrap")

    frame_num = int((len(waveform) - frame_length) / hop_length) + 1
    waveform_zcr = []

    for t in range(frame_num):
        current_frame = waveform[(frame_length - hop_length) * t : (frame_length - hop_length) * t + frame_length]
        a = np.sign(current_frame[0 : frame_length - 1, ])
        b = np.sign(current_frame[1 : frame_length, ])

        current_zcr = np.sum(np.abs(a - b)) / 2 / frame_length
        waveform_zcr.append(current_zcr)

    return np.array(waveform_zcr)

# 3.设置参数: 每一帧长 1024, 以 50% 的重叠半分帧, 调用该函数
frame_size = 1024
hop_size = int(frame_size * 0.5)
waveform_ZCR = Calc_ZCR(waveform, frame_size, hop_size)

# 4.绘制图像
frame_scale = np.arange(0, len(waveform_ZCR), step = 1)
time_scale = librosa.frames_to_time(frame_scale)
plt.figure(figsize = (20, 10))
librosa.display.waveshow(waveform)
plt.plot(time_scale, waveform_ZCR, color = "r")
plt.title("Zeri-Cross-rate")
plt.show()

# 5.利用自带函数
waveform_zcr_librosa = librosa.feature.zero_crossing_rate(y=waveform, frame_length=frame_size, hop_length=hop_size).T[1:, 0]
plt.figure(figsize = (20, 10))
librosa.display.waveshow(waveform)
plt.plot(time_scale, waveform_zcr_librosa, color = "r")
plt.title("Zeri-Cross-rate")
plt.show()

# 6.比较差异
bias = waveform_zcr_librosa - waveform_ZCR
print(f"the bias is {bias} !!!!")

第五章信号的频域分析谱质心与子带带宽

频域分析：将信号的时域转换为频域
- 傅里叶变换：离散 / 连续均可
- 拉普拉斯变换：应用于连续信号
- Z 变换：应用于离散信号
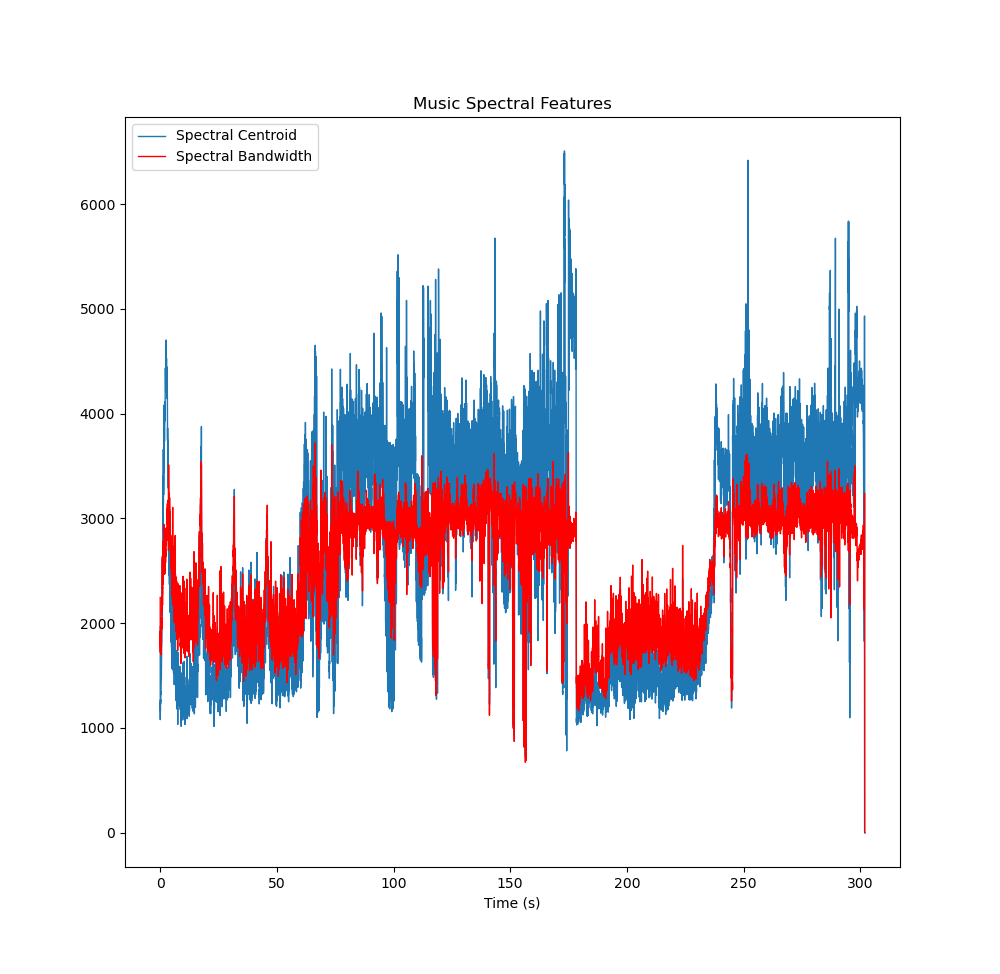
谱质心 Spectral centroid：是频率成分的重心，是频谱中在一定频率范围内通过能量加和权平均的频率，其单位是 Hz。
- 可以用来描述声音的主观听觉：谱质心低，则声音信号低沉；谱质心高，则声音信号明亮
- 该参数常用于对乐器声色的分析研究

子带带宽 Bandwidth
- 操作：在 Spectral centroid 的频谱范围，计算每一点到谱质心的的距离的加权平均值。
- BW = 每个采样点减去谱质心的绝对值 * 对应点的权重值 / 总的权重之和（注意：权重为人工设置）
- 应用：用于音频识别和主观听音感受，如果音频的能量谱密度函数下降快，那么BW也下降，类似于频谱的变化速度。

代码演示

  
'''
信号的频域特征
# 1.加载信号
# 2.获得信号的 Spectral centroid 和 bandwidth
 librosa.feature.spectral_centroid(y = waveform)
# 3.获得信号的 Spectral bandwidth
 librosa.feature.spectral_bandwidth(y = waveform)
'''

# 0.预设环境
import librosa
import numpy as np
from matplotlib import pyplot as plt
import librosa.display
import seaborn as sns

# 1.加载信号
music_path = "D:\\02-programme_BJTU_New\\DeepLearning\\ASP_DL\\test_audio.mp3"
music, sr = librosa.load(music_path)

# 定义 hop_length
hop_length = 512

# 2.获得信号的 Spectral centroid 和 bandwidth
sc_music = librosa.feature.spectral_centroid(y=music, n_fft=1024, hop_length=hop_length).T[:, 0]

# 3.获得信号的 Spectral bandwidth
sw_music = librosa.feature.spectral_bandwidth(y=music, n_fft=1024, hop_length=hop_length).T[:, 0]
# n_fft 是 FFT 快速傅里叶变换窗口大小的参数
# 窗口越大，时间分辨率越低，因为更大的窗口会覆盖更长的时间段，导致时间上的细节被平滑掉。
# 原本是 (1, 13006) 需要转置 + 只取一维

# 计算时间
t = np.arange(0, len(sc_music)) * (hop_length / sr)

fig, ax = plt.subplots(figsize=(10, 10))
ax.plot(t, sc_music, linewidth=1, label="Spectral Centroid")
ax.plot(t, sw_music, linewidth=1, color="r", label="Spectral Bandwidth")
ax.set_title("Music Spectral Features")
ax.set_xlabel('Time (s)')
ax.legend()
plt.show()

第六章信号的时频分析 - STFT 短时傅里叶变换

常见方法:短时傅里叶变换、小波变换、Wigner-Ville 时频分布及 HHT 等
结果:得到不同时间、频率处信号的幅值和相位,很好地分析了实际音频信号的非平稳非线性特点。
STFT - Short-Time Fourier Transform - 短时傅里叶变换
- 由于声信号往往是随时间变化的，在短时间内可以近似看做平稳（对于语音来说是几十毫秒的量级），所以我们希望把长的声音切短，来观察其随时间的变化情况己，由此产生 STFT 分析方式
- 得到不同时刻，不同频率的频谱图（能量分布情况）
FFT 与 STFT对比:
- STFT在时域中对信号进行加窗处理（分帧），所以最终结果是有关时域频域的信息，时域的信息是每一帧帧长）窗函数的长度）
- 加入了 τ，对应窗函数的长度

时频域之间存在测不准原理：
- 举例：无限长矩形窗函数，做傅里叶变换，得到冲激函数；冲激函数做傅里叶变换，得到形如 sin 的函数
- 要精确测量信号的频率，需要让信号持续足够长的时间，以便观察到完整的周期变化，这意味着在时域上信号不能被局限在一个很短的区间内，否则无法准确分辨其频率成分。相反，若要在时域上精确确定信号发生的时刻，那么信号在频域上就会变得较为宽泛，因为窄的时域脉冲包含了丰富的高频成分，其频率范围会很广。
- 我们做不到让信号“既短又长”，即做不到同时精确测量时域与频域

代码演示

  
'''
# 信号的 STFT 短时傅里叶变换
# 1.加载信号
# 2.信号分帧；补零 -> 加窗 -> 分帧
# 3.信号做傅里叶变换 np.fft.rfft(waveform_frame,n_fft)
# waveform_fft = пр.fft.rfft(waveform_win,n_fft)
# 4.功率谱函数 waveform_pow = np.abs(waveform_fft)**2/n_fft
# waveform_db = 20* np.log10(waveform_pow)
# 5.绘制波形
'''

# 0.预设环境
import librosa
import numpy as np
from matplotlib import pyplot as plt
import librosa.display
import seaborn as sns

# 1.加载信号
wave_path = "D:\\02-programme_BJTU_New\\DeepLearning\\ASP_DL\\test_audio.mp3"
waveform, sample_rate = librosa.load(wave_path)

# 2.信号分帧；补零 -> 加窗 -> 分帧
frame_size, hop_size = 1024, 512
if len(waveform) % hop_size != 0:
    frame_num = int((len(waveform) - frame_size) / hop_size) + 1
    pad_num = frame_num * hop_size + frame_size - len(waveform)
    waveform = np.pad(waveform, pad_width = (0, pad_num), mode = "wrap")

frame_num = int((len(waveform) - frame_size) / hop_size) + 1

# 分帧
row = np.tile(np.arange(0, frame_size), (frame_num, 1))
# 这行代码的作用是利用 numpy 的 arange 和 tile 函数生成一个二维数组，其中每一行都是一个从 0 到 frame_size - 1 的序列，并且这样的行重复了 frame_num 次。

column = np.arange(0, frame_num * (frame_size - hop_size), (frame_size - hop_size))
# 生成一个数组，表示每一帧的起始位置，帧之间的间隔为 frame_size - hop_size，总共生成 frame_num 个起始位置。

column = np.tile(column, (frame_size, 1)).T
index = row + column # 各元素相加
waveform_frame = waveform[index]

# 加窗
waveform_frame = waveform_frame * np.hanning(frame_size)
# 这句代码的核心作用是通过 Hanning 窗对信号帧进行加权，减少边界效应，为后续的信号处理（如傅里叶变换）做好准备。这是信号处理中的常见操作

# 3.信号做傅里叶变换
n_fft = 1024
waveform_stft = np.fft.rfft(waveform_frame, n_fft)

# 4.功率谱函数
waveform_pow = np.abs(waveform_stft) ** 2 / n_fft
min_value = 1e-10
waveform_pow = np.maximum(waveform_pow, min_value)
waveform_db = 20 * np.log10(waveform_pow) # 功率谱函数转换为分贝

# 5.绘制波形
plt.figure(figsize=(10, 10))
# 计算时间和频率范围
time = np.arange(0, frame_num) * hop_size / sample_rate
freq = np.linspace(0, sample_rate / 2, int(n_fft / 2) + 1)
# 使用 imshow 绘制时频图，并设置 extent 参数
plt.imshow(waveform_db, aspect='auto', origin='lower', extent=[time.min(), time.max(), freq.min(), freq.max()])
plt.colorbar(format='%+2.0f dB')
plt.xlabel('Time (s)')
plt.ylabel('Frequency (Hz)')
plt.title("Waveform_STFT")
plt.show()

第七章信号的时频分析STFT及小波变换

使用 librosa 绘制 STFT

代码演示

  
import numpy as np
from matplotlib import pyplot as plt
import librosa

# 时域
def plot_waveform(waveform, sr, title = "Waveform"):
    waveform = np.array(waveform)
    samples = waveform.size
    time_scale = np.linspace(0, samples / sr, num = samples)
    plt.figure(figsize = (20, 10))
    plt.plot(time_scale, waveform, linewidth = 1)
    plt.title(title)
    plt.show()

# 频域
def plot_waveform_fft(waveform, sr, n_fft, title = "Waveform_FT"):
    waveform = np.array(waveform)
    samples = waveform.size
    waveform_fft = np.fft.rfft(waveform, n_fft)
    freq_scale = np.linspace(0, sr / 2, num = int(n_fft / 2) + 1)
    plt.figure(figsize = (20, 10))
    plt.plot(freq_scale, waveform_fft, linewidth = 1)
    plt.show()

# 二维
def plot_spectrogram(spectrogram, title = "Spectrogram(dB)"):
    plt.imshow(librosa.amplitude_to_db(spectrogram), )
    plt.title(title)
    plt.xlabel("Frame / s")
    plt.ylabel("Frequency")
    plt.colorbar()
    plt.show()

小波变换 - 另一种变换方式
- 对于不稳定的信号，难以用普通的FFT分析出频域随时变化的信息。
- 所以对于不同时间段的频域函数进行分析，利用小波作为基函数，各个小波函数按照不同比例系数展开得到 F，其中小波函数可以更改中心频率和带宽。
- 操作:将欧拉函数置换成小波函数,小波函数随着原信号会发生变化
STFT 与小波变换对比：
- STFT分帧的窗函数是固定时长，相同窗长分帧的过程使频率分辨率就会降低。因为分帧也就是加窗的过程,由于窗函数长度有限的，会造成截断。窗函数长，则时间分辨率低，而频率分辨率高；窗函数短，则频率分辨率低，而时间分辨率高；
- 小波变换通过更改小波函数的带宽，设置不同的基频，因此不同频颜段利用不同的分辨率。在低频成分用高的频率分辨率；高频成分用高的时间分辨率。

PART 2 - Python + Pytorch 知识

第八章 - 消失了 QWQ

第九章 - Pycharm 编译环境介绍

我不造啊我用 Vscode 的

第十章 - 张量 tensor 的使用

张量，可以在 GPU 或者其它专用硬件上运行

第十一章 - 无继承型类 Class 的使用

定义自己的类(无继承) – 定义可调用的类
利用已存在的类，定义自己的类（模板）
注意：一般情况在 python 中函数，函数类都是可调用的。至于由类生三成的对象，是否是可调用的，主要是看类中是否有实现魔术方法 _call_。

  
myclass() # 即可直接调用 __call__

第十二章 - 数据集的类 Dataset 的使用

请见小土堆 pytorch Dataset 详解

第十三章 - 数据集 UrbanSound8k

PART 3 - 机器学习 + 神经网络知识

第十八章 - 机器学习及深度学习介绍

第十九章 - 神经网络原理

第二十章 - 构建感知器及神经网络中的浅层学习

构建感知器
- 感知器：包含参数 w 和 b 的激活函数，网络神经的最基本单元
- 按权重分配后，将结果送到激活函数（也称为传递函数）得得到输出
- Sigmoid: y = 1 / (1 + math.exp(-y))

感知器代码演示

  
import math

def neuron(input, weight, bias):
    output = 0
    for x, w in zip(input, weight):
        output += w * x
    output = output + bias
    output = 1 / (1 + math.exp(-output))
    return output

神经网络中的浅层学习
- 最主要的特点是模型简单，包含输入层，隐藏层和输出层

浅层学习代码演示

  
"""定义浅层学习网络函数(含两个运算层)
# shallow_learning(input, weight1, weight2, bias1, bias2):
# 1.定义线性部分 output1 = np.sum(input * weight) + bias
# 2.定义非线性激活部分 output1 = 1 /(1 + np.exp(-output1) )
# 3.给定输入与权重系数，得到输出
"""

import math
import numpy as np

class ShallowNet:
    def __init__(self, weight1, bias1, weight2, bias2):
        self.weight1 = weight1
        self.bias1 = bias1
        self.weight2 = weight2
        self.bias2 = bias2

    def calculate(self, x):
        output = np.dot(x, self.weight1) + self.bias1
        output = 1 / (1 + np.exp(-output))

        y = np.dot(output, self.weight2) + self.bias2
        y = 1 / (1 + np.exp(-y))

        return y

第二十一章 - 神经网络中的深度学习

  
import numpy as np

class DeepNet:
    def __init__(self, input_num, out_num, hidden_num):
        self.model = [input_num] + hidden_num + [out_num]
        self.weight = []
        self.layer_num = len(self.model)
        for i in range(self.layer_num - 1):
            current_weight = np.random.rand(self.model[i], self.model[i + 1])
            self.weight.append(current_weight)
        self.bias = 0

    def calculate(self, data):
        for w in self.weight:
            y = np.dot(data, w)
            y = 1 / (1 + np.exp(-y))
            data = y
        return y

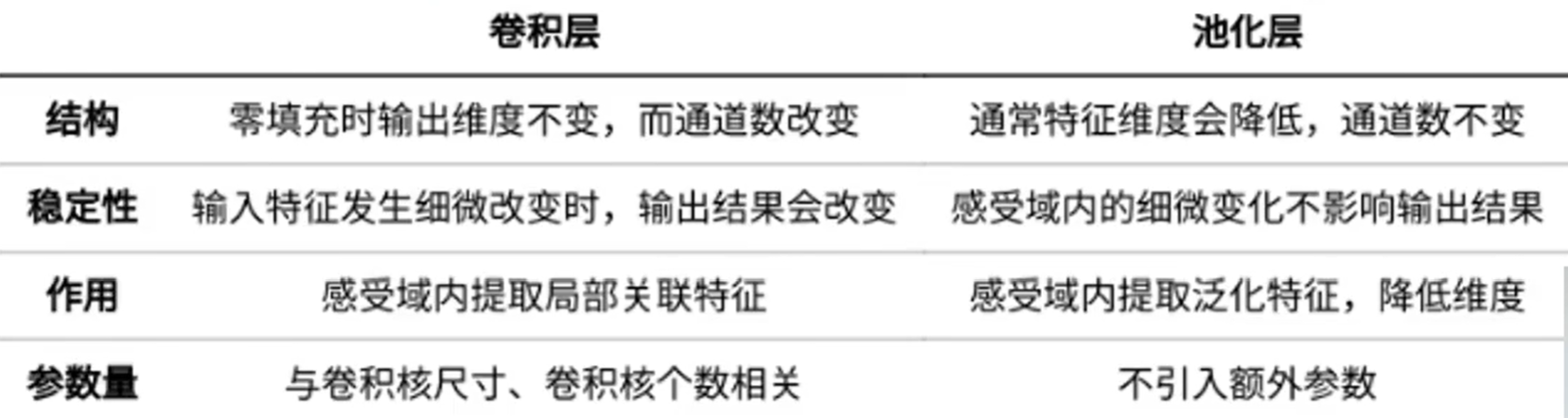
第二十二章 - 构造隐藏层之卷积层

概念：利用卷积核（kernel）实现数据的特征提取。
实际操作：按照一定权重处理输入对象并累加。与信号处理中的卷积有些不同，这里不存在时间反演，只是简单的相乘累加

第二十三章 - 构造隐藏层之池化层

概念：也叫汇聚层，用于压缩数据和参数的量减小过拟合。也就是在不改变数据特征的情况下，将数据的尺寸变少。
具体作用:
- 特征不变性：将图片缩小，但其特征的含量不变
- 特征降维：把这类冗余信息去除，把最重要的特征抽取出来
- 在一定程度上防止过拟合，更方便优化
常见的池化层：最大池化，均值池化等

第二十四章 - 构造隐藏层之非线性层ReLU, Tanh, Sigmoid

概念：因为只有若干线性层，其堆叠只能起到线性映射的作乍用，无法形成复杂的函数，因此引入非线性激活层

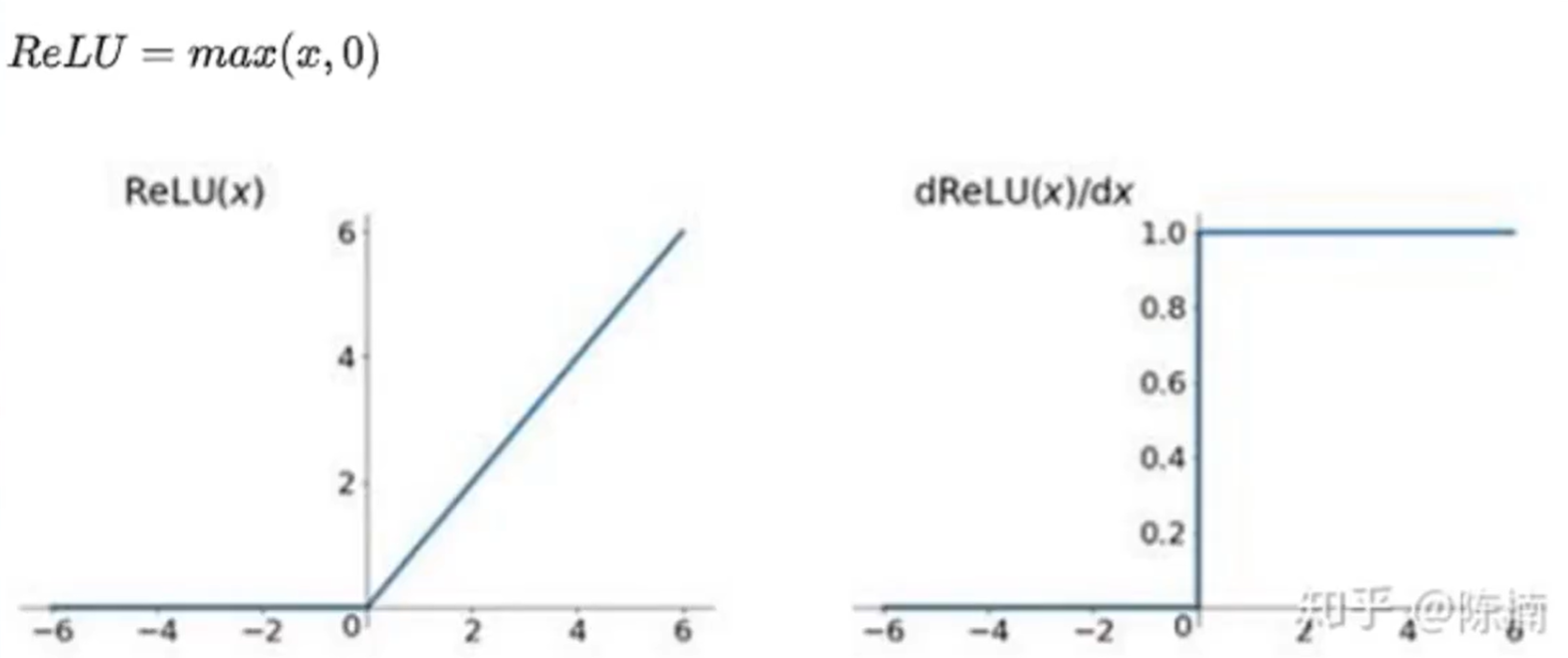
ReLU

优点：解决梯度消失的问题（其导数是非 0 值），计算速度快（只有输出 0, 1）
缺点：没有输出负数，不是 zero-centered，可能会出现 Dead ReLU Problem，也就是一些神经元不会被激活到。因为计算速率太高导致训练过程中参数更新太快。

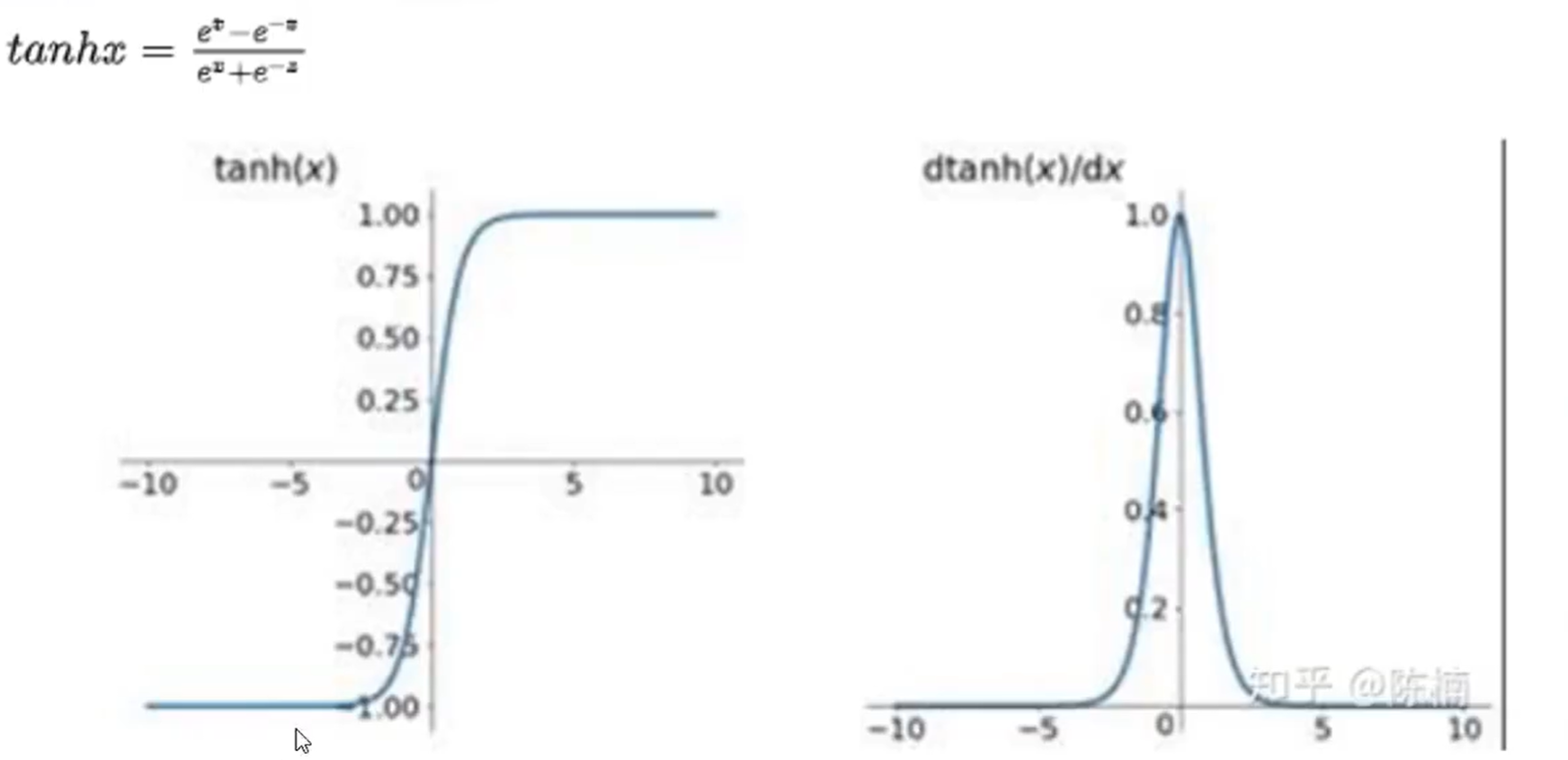
Tanh

优点：输出正负，解决了 zero-centered 的输出问题
缺点：梯度消失的问题和幂运算的问题仍然存在

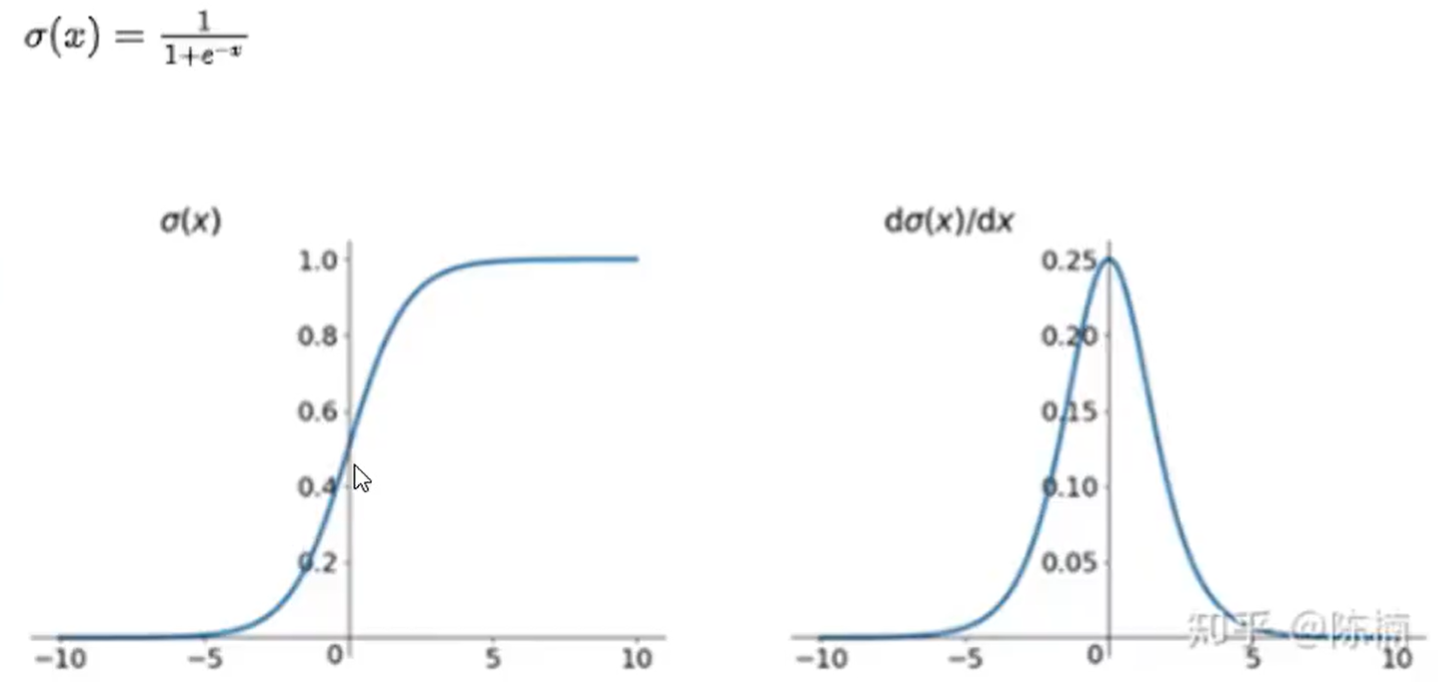
Sigmoid

优点：适用于多分类问题，将输出值归一化
缺点：可能会产生梯度消失，并且权重更新过程不是一个收敛的过过程，Sigmoid 函数的输出值恒大于 0，这会导致模型训练的收敛速度变慢

第二十五章 - 构造完整的神经网络及小结

请见小土堆 pytorch 搭建实战

第二十六章 - 神经网络训练原理

线性层：nn.Linear(in_features, out_features)

请见小土堆 pytorch nn.modules 中 nn.Linear 详解

PART 4 - 神经网络训练知识

第二十七章 - 逼近的思路理解神经网络的训练_损失函数与自动求梯度 Autograd

第二十八章 - 逼近的思路理解网络训练_更新模型参数

第二十九章 - 逼近的思路理解网络训练_优化器

A. 常规方法

思路：根据预测值与标签值得到loss -> loss函数对各个参数反向求偏导 -> 计算每个参数的梯度 -> 更新参数值 -> 梯度置零 -> 再次循环

B. loss.backward()

思路：根据预测值与标签值得到 loss -> loss 函数对各个参数反向求偏导 -> loss.backward() 自动更新参数的梯度 -> 更新参数值 -> 梯度置零 -> 再次循环
区别：每个参数的 grad 值是自动计算
功能：误差张量上调用 .backward() 时，开始反向传播。然后，Autograd会为每个模型参数计算梯度并将其存储在参数的 .grad 属性中。

C. optimiser.step()

思路：根据预测值与标签值得到 loss -> loss 函数对各个参数反向求偏导 -> loss.backward()自动更新参数的梯度 -> optimiser.step() 更新参数值 -> 梯度置零 -> 再次循环
区别：每个参数值是自动更新
功能：调用 .step() 启动梯度下降。优化器通过 .grad 中存储的梯度来调整每个参数

第三十章 - 网络训练_损失函数与优化器

常用的损失函数：

平方损失，sum(输出值 - 预期值)的平方，找出最小的二乘得到的值。

最大似然处理，将输出的结果（似然值）视为概率，再去求得到该结果概率值最大的权重系数 w。已知事情发生的结果，反推发生该结果概率最大的参数 w P(x

w,b)

交叉熵损失：交叉熵越小，两个模型最相似

常用的优化器：
- SGD：Stochastic Gradient Descent，随机梯度下降
- Adam：Adaptive Moment Estimation，自适应矩估计

代码演示

  
import torch

loss_l1 = torch.nn.L1Loss(reduction="sum")
result1 = loss_l1(y_pred, y)

loss_mse = torch.nn.MSELoss(reduction="sum")
result2 = loss_mse(y_pred, y)

第三十一章 - 网络模型搭建与训练整个过程

请见小土堆 pytorch 搭建实战
或见 Resnet 复现实例

AI + MUSIC, Basic knowledge

ai music

This post is licensed under CC BY 4.0 by the author.

课程内容

PART 1 - 信号分析

第一章 信号分析简介

信号分析是什么

为什么要分析信号

信号分析方式

多个信号的叠加

第二章 信号的时域分析幅值包络

幅值包络

分帧概念

代码演示

第三章 信号分析简介

均方根能量 Root mean square energy

代码演示

第四章 信号的时域分析过零率

代码演示

第五章 信号的频域分析谱质心与子带带宽

代码演示

第六章 信号的时频分析 - STFT 短时傅里叶变换

代码演示

第七章 信号的时频分析STFT及小波变换

代码演示

PART 2 - Python + Pytorch 知识

第八章 - 消失了 QWQ

第九章 - Pycharm 编译环境介绍

第十章 - 张量 tensor 的使用

第十一章 - 无继承型类 Class 的使用

第十二章 - 数据集的类 Dataset 的使用

第十三章 - 数据集 UrbanSound8k

第十四章 - 数据集的类 Dataloader 的使用

第十五章 - SummaryWriter 类写函数及音频

第十六章 - SummaryWriter 类写图像

第十七章 - 网络结构的类 nn.Module nn.Sequential

PART 3 - 机器学习 + 神经网络 知识

第十八章 - 机器学习及深度学习介绍

第十九章 - 神经网络原理

第二十章 - 构建感知器及神经网络中的浅层学习

感知器代码演示

浅层学习代码演示

第二十一章 - 神经网络中的深度学习

第二十二章 - 构造隐藏层之卷积层

第二十三章 - 构造隐藏层之池化层

第二十四章 - 构造隐藏层之非线性层ReLU, Tanh, Sigmoid

ReLU

Tanh

Sigmoid

第二十五章 - 构造完整的神经网络及小结

第二十六章 - 神经网络训练原理

PART 4 - 神经网络训练 知识

第二十七章 - 逼近的思路理解神经网络的训练_损失函数与自动求梯度 Autograd

第二十八章 - 逼近的思路理解网络训练_更新模型参数

第二十九章 - 逼近的思路理解网络训练_优化器

A. 常规方法

B. loss.backward()

C. optimiser.step()

第三十章 - 网络训练_损失函数与优化器

代码演示

第三十一章 - 网络模型搭建与训练整个过程

Trending Tags

第一章信号分析简介

第二章信号的时域分析幅值包络

第三章信号分析简介

第四章信号的时域分析过零率

第五章信号的频域分析谱质心与子带带宽

第六章信号的时频分析 - STFT 短时傅里叶变换

第七章信号的时频分析STFT及小波变换

PART 3 - 机器学习 + 神经网络知识

PART 4 - 神经网络训练知识